Counter space is the space in which subtle forces work, such as those of life, which are not amenable to ordinary measurement. It is the polar opposite of Euclidean space. It was discovered by the observations of Rudolf Steiner and described geometrically by George Adams and, independently, by Louis Locher-Ernst. Instead of having its ideal elements in a plane at infinity it has them in a "POINT at infinity". They are lines and planes, rather than lines and points as in ordinary space. We call this point the counter space infinity, so that a plane incident with it is said to be an ideal plane or plane at infinity in counter space. It only appears thus for a different kind of consciousness, namely a peripheral one which experiences such a point as an infinite inwardness in contrast to our normal consciousness which experiences an infinite outwardness.
Nick Thomas has explored the idea that objects existing in both spaces at once are subject to strain and stress, and an analysis of these leads to new approaches to gravity and other forces as summarised in the diagram below. The pentagons are 'hot spots' to explore further.
LINKAGES
A linkage is an element that belongs to both Euclidean- and counter-space at once e.g. a point or plane. Suppose a cube is linked to both spaces at once, and is moved upwards away from the inner infinitude. It will try to obey the metrics of both spaces, and the diagram below shows what happens as it moves, the yellow version obeying space and staying the same size and shape in space, while the magenta version obeys the counter space metric.

The counter space- or inner-infinity is shown as a point at the bottom, and lines have been drawn from it through the vertices of the cube. The counter-spatial movement is such that the vertices stay on these lines in order to obey its metric properties, as illustrated by the magenta cube, while the spatial one stays the same spatially. With our ordinary consciousness that is what seems natural, of course, but for a counter space consciousness the other is most natural and the yellow cube appears to be getting bigger (NOT smaller!!). The geometric difference between the two cubes is referred to as strain, analogously to the use of that term in engineering where it is the percentage deformation in size when, for example, an elastic band is stretched. The elastic band responds to the strain by exerting a force, which is referred to as stress. The central thesis here is thus:
1. Objects may be linked to both spaces at once,
2. When they are, strain arises when they move as the metrics are conflicting,
3. Stress arises as a result of the strain.
Note well that stress is not a geometric concept, and we move from geometry to physics when we consider stress. The major stress-free movement or transformation is rotation about an axis through the counter space infinity, which may explain the ubiquitous appearance and importance of rotation in most branches of physics e.g. in fluid flow.
This, and all else in the pages concerned with counter space, is explained in more detail in Science Between Space and Counterspace (Algebraic Projective Geometry , Semple and Kneebone, Oxford University Press, Oxford 1952.). Some algebraic details are given in the subordinate algebraic page.
ALGEBRAIC APPROACH TO COUNTERSPACE
Polariy and Quadric Surfaces
The basic algebra for handling projective geometry is introduced in the Basics page. Important is the duality it so clearly expresses which enables the concept of polarity to be handled conveniently. The equation of a quadric surface is a general homogeneous equation of the second degree in the homogeneous coordinates (x, y, z, w):
In matrix form this is

which may be expressed as x'Qx = 0 where x is a column vector, x' is the corresponding row vector and Q is the symmetrical 4x4 matrix representing the quadric surface. Now consider the equation y'Qx = 0. We may regard Qx as the coordinates u of a plane so that y'u = 0 simply expresses the fact that Y lies in U (using Y to denote the geometric point represented by y, etc.). Now Y need not lie on Q, so the expression requires it to lie in the plane U, and any value of x that ensures that satisfies the equation. As X varies in accordance with this we obtain all the planes U in Y. Looking at the situation the other way round, y'Q is also a plane, moreover a fixed plane v since Y is fixed, and as vx = 0, all the points X must lie in V. Thus for every fixed point Y the quadric Q determines a plane of points which is the polar plane of Y. Conversely given a plane V, v = y'Q for a unique point Y, since y' = Q"v determines Y uniquely, where Q" is the inverse matrix of Q. Y is the pole of V, and this polar relationship is one-to-one provided the quadric is not singular. If Y lies on Q then one solution for x is x = y as then y'Qy = 0 by definition of the quadric, so the plane Qy is the tangent plane at Y since no other point X can satisfy y'Qx = 0 and lie on the surface. If Y lies outside the quadric then planes U exist which touch Q in which case, by what we have just seen, X lies on Q (recalling that X is given by u = Qx). This corresponds to the diagram in the Basics page where the polar of Y intersects Q when Y lies outside Q, and conversely if Y lies inside Q then no real plane U can be a tangent plane so V does not intersect Q.
A quadric may also be expressed in terms of plane coordinates as follows. In x'Qx = 0, u' = x'Q touching at x, and u = Qx also touching at x. Thus x'Qx = x'QQ"Qx = u'Q"u = 0, giving the class quadric as the envelope of its tangent planes U, which is the same as the surface described by X. This connection is only valid for non-singular quadrics, but of course any quadric also has a class equation, singular or not (e.g. a cone possesses tangent planes). A slight economy is possible as it is not necessary to divide by the determinant of Q when deriving Q" since we are using homogeneous coordinates, so in the literature we usually find the class quadric expressed as u'(Q)u = 0 where (Q) is the adjoint matrix of Q.
Projective Classification of Quadrics
There are three distinct types of quadric in purely projective geometry, distinct because no real projective transformation can transform a member of one type into a member of another. By suitable change of coordinates it is possible to reduce the equation of the quadric to canonical form where only the terms in the leading diagonal of Q are non-zero. This gives an equation
which is singular if any of a b c or d is zero (cones if one is zero, plane pairs if two are zero, two coincident planes for three zero).
Three possibilities exist for the relative signs of a b c and d:
- one of opposite sign to the other three,
- two positive and two negative,
- all of the same sign.
In the first case, taking d to be negative and reverting to Cartesian coordinates by dividing by w2, we have ax2 + by2 + cz2 = d which is the equation of an ellipsoid. A similar result is obtained if instead a b or c is negative, recalling that infinity is not invariant so all central quadrics are projectively equivalent.
In the second case, setting a=A2 etc. such that A B C D are all positive, we have for example when b and d are negative the equation (Ax + By)(Ax - By) = (Cz + Dw)(Cz - DW). This is satisfied by any line which is the intersection of the two planes Ax+By-Cz-Dw = 0 and Ax-By-Cz+Dw = 0, and also by the plane pairs Ax+By-Cz+Dw = 0, AX-By-Cz-Dw = 0. It is thus a ruled quadric, the two alternatives yielding the two complementary sets of generators.
In the third case the quadric contains no real points and is accordingly purely imaginary.
Projective Geometry may also be studied by means of algebra.
Projective Geometry may also be studied by means of algebra. Linear transformations are expressed as matrices, and the transformation of a point or plane is accomplished by multiplying the vector representing it by the transformation matrix.
HOMOGENEOUS COORDINATES
The Cartesian coordinates of a point may be expressed as (x,y,z) with respect to the three orthogonal axes. The problem encountered in using them, however, is that ideal points at infinity cannot be handled because x,y or z (or all three) become infinite. If a point moves towards infinity in a fixed direction then the ratios x : y : z remain constant. We may introduce a fourth number w and re-express the coordinates as x/w : y/w : z/w, noting that the ratios are unaffected. If we multiply all coordinates by a constant k the ratios are still unaffected. We now re-express the point as (x,y,z,w) as if we were working in four dimensions i.e. we regard w as a fourth coordinate. If w becomes zero then we see that x/w, y/w and z/w each become infinite to give us a point at infinity, but instead of retaining these improper ratios we instead express that fact as (x,y,z,0). This formulation retains intact the ratios of x : y : z of the point before it reached infinity, and we use w=0 to indicate we have gone to infinity. Thus for each direction in space (x,y,z,0) is unique, the twofold infinity of ratios x : y : z representing that direction and (x,y,z,0) its ideal point. Two aspects should be noted:
- (x,y,z,1) returns us to the Cartesian coordinates when w=1 is discarded;
- (kx,ky,kz,kw) is the same point as (x,y,z,w) as we are now only interested in ratios.
These coordinates are known as homogeneous coordinates because they still refer to three dimensions despite the use of four coordinates, and the coordinates are homogeneous in the sense that they are are not absolute but enter into equations fully symmetrically, just as a homogeneous equation contains all products of its variables to a fixed overall power.
(x,0,0,0) is the point at infinity on the x-axis, and similarly for the y and z axes.
Since we may divide throughout by k=x this simplifies to (1,0,0,0).
(0,0,0,1) is the origin.
Once we switch to homogeneous coordinates the axes need not remain orthogonal, and we end up with a tetrahedron of reference with vertices (1,0,0,0), (0,1,0,0), (0,0,1,0) and (0,0,0,1). All connection with Cartesian coordinates is then lost as distances can no longer be associated with x,y,z and w. This expresses the non-metric nature of projective geometry. The infinite plane is no longer defined as the plane w=0 but can be any face of the tetrahedron, consistent with the fact that an infinite plane is not defined for projective geometry, only for affine and metric geometry.
DUALITY
If we take y=0 then we have all the points in the XZW plane. If we take x+y=0 then we have all the points in the plane for which x=-y. Generally a linear equation in x,y,z,w yields a plane i.e.
kx + ly + mz + nw = 0
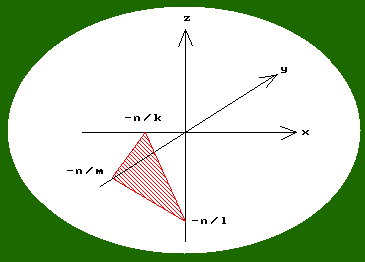
for constant k,l,m,n is the equation of a plane. Now suppose we hold x,y,z,w constant and vary k,l,m,n while satisfying the equation. Clearly we obtain all possible quadruples (k,l,m,n) satisfying the equation for that fixed point (x,y,x,w) i.e. all possible planes containing (x,y,x,w), from which it is clear that (k,l,m,n) may be regarded as the coordinates of the planes. The duality of point and plane is beautifully expressed by the symmetry of the equation. The meaning of these coordinates may be appreciated if we think of the Cartesian special case with w=1. On the x-axis y=z=0 so x=-n/k, and similarly on the y- and z-axes, so the plane represented by the coordinates is as illustrated below.
Books related to COUNTER-SPACE:
🌀 Applications of electromagnetic theory in the Ether field:
Two types of power generation technology (generator) of Nikola Tesla
- 🔹 Radiant energy
- 🔹 AC generator - Free Energy
🔹 Tesla Technology and "Free Energy" in practical application